Max-Usa
Site Yöneticisi
- Katılım
- 31 Ağu 2023
- Mesajlar
- 46,079
- Tepkime
- 53,102
- Puanları
- 1,220
- Konum
- TÜrkiye -Ege -İzmir
- Coin
- 112,329
Altmışlık sayı sistemi , 60 tabanlı olarak da bilinir , [ 1 ] tabanı altmış olan bir sayı sistemidir . MÖ 3. binyılda antik Sümerler tarafından ortaya çıkarılmış, antik Babillilere aktarılmıştır ve hala zamanı , açıları ve coğrafi koordinatları ölçmek için değiştirilmiş bir biçimde kullanılmaktadır .
Üstün, oldukça bileşik bir sayı olan 60 sayısının on iki böleni vardır : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ve 60; bunlardan 2, 3 ve 5 asal sayılardır . Bu kadar çok çarpanı olması nedeniyle, altmışlık sayıları içeren birçok kesir basitleştirilir. Örneğin, bir saat 30 dakika, 20 dakika, 15 dakika, 12 dakika, 10 dakika, 6 dakika, 5 dakika, 4 dakika, 3 dakika, 2 dakika ve 1 dakikalık bölümlere eşit olarak bölünebilir. 60, 1'den 6'ya kadar her sayıya bölünebilen en küçük sayıdır; yani, 1, 2, 3, 4, 5 ve 6'nın en küçük ortak katıdır .
Bu makalede, aksi belirtilmediği sürece tüm altmışlık basamaklar ondalık sayılar olarak temsil edilir. Örneğin, en büyük altmışlık basamak "59"dur.
Kökeni
Otto Neugebauer'e göre , altmışlık sayı sisteminin kökenleri, sıklıkla tasvir edildiği kadar basit, tutarlı veya zamansal olarak tekil değildir. Günümüzde zaman, açılar ve astronomik koordinat sistemleri gibi uzmanlaşmış konular için kullanılmaya devam eden yüzyıllar boyunca, altmışlık sayı sistemi gösterimleri, altmışlık sayı sisteminin nasıl yazıldığı gibi konularda her zaman güçlü bir ondalık gösterim alt akıntısı içermiştir. Kullanımları ayrıca, tek bir metin içinde bile sayıları temsil etmek için çeşitli tabanların nerede ve nasıl kullanılacağı konusunda tutarsızlıklar içermiştir (ve içermeye devam etmektedir). [ 2 ]
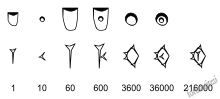
Erken Proto-çivi yazısı (M.Ö. 4. bin yıl) ve altmışlık sisteme ait çivi yazısı işaretleri (60, 600, 3600, vb.)
Altmışlık sistemin titiz ve tamamen kendi içinde tutarlı bir şekilde kullanılmasının en güçlü itici gücü, kesirleri yazma ve hesaplama konusundaki matematiksel avantajları olmuştur. Antik metinlerde bu, altmışlık sistemin matematiksel veri tablolarında en tekdüze ve tutarlı şekilde kullanılması gerçeğinde ortaya çıkar. [ 2 ] Altmışlık sistemin geçmişte matematiksel tablolarda olduğundan daha az tutarlı bir şekilde kullanılmasına rağmen kullanımının yaygınlaşmasına yardımcı olan bir diğer pratik faktör, büyük miktarlarda mal için pazarlık yapmayı ve bunları paylaşmayı içerdiğinde günlük finansal işlemleri kolaylaştırması açısından tüccarlar ve alıcılar için belirgin avantajlarıydı. MÖ 3. binyılın sonlarında, Sümer/Akad ağırlık birimleri, 60 manû'ya ( mina ) bölünen kakkaru'yu ( talent , yaklaşık 30 kg) içeriyordu ve bu da daha sonra 60 šiqlu'ya ( şekel ) bölündü ; bu birimlerin torunları binlerce yıl boyunca varlığını sürdürdü, ancak Yunanlılar daha sonra bu ilişkiyi bir şekelin bir minanın 50'de biri olduğu daha taban-10 uyumlu bir orana zorladı .
Matematiksel tabloların dışında, sayıların çoğu metinde nasıl temsil edildiğine ilişkin tutarsızlıklar , sayısal nicelikleri temsil etmek için kullanılan en temel çivi yazısı sembollerine kadar uzanıyordu . [ 2 ] Örneğin, 1 için çivi yazısı sembolü, kalem ucunun yuvarlak ucunun kile açılı olarak uygulanmasıyla oluşturulan bir elips iken, 60 için altmışlık sembol daha büyük bir oval veya "büyük 1" idi. Ancak bu sembollerin kullanıldığı aynı metinlerde, 10 sayısı, stilin yuvarlak ucunun kile dik olarak uygulanmasıyla oluşturulan bir daire olarak temsil ediliyordu ve 100'ü temsil etmek için daha büyük bir daire veya "büyük 10" kullanılıyordu. Bu tür çok tabanlı sayısal nicelik sembolleri, tek bir sayı içinde bile birbirleriyle ve kısaltmalarla karıştırılabiliyordu. Ayrıntılar ve hatta ima edilen büyüklükler ( sıfır tutarlı bir şekilde kullanılmadığından ) temsil edilen belirli zaman dilimlerine, kültürlere ve niceliklere veya kavramlara özgüydü. Sayısal niceliklerin bu tür bağlam-bağımlı temsillerinin geriye dönüp bakıldığında eleştirilmesi kolay olsa da, modern zamanlarda, altmışlık astronomik koordinatlara ondalık kesirlerin eklenmesi gibi son yenilikler de dahil olmak üzere, konuya-bağımlı temel karıştırmanın düzenli olarak kullanılan düzinelerce örneğine hâlâ sahibiz. [ 2 ]
Kullanım
Babil matematiği
Ana madde: Babil çivi yazısı rakamları
Antik Mezopotamya'da kullanılan altmışlık sistem , rakamları için 60 ayrı sembol kullanmadığı anlamında saf bir 60 tabanlı sistem değildi . Bunun yerine, çivi yazısı rakamları bir işaret-değer gösterimi tarzında alt taban olarak on kullanıyordu : bir altmışlık rakam, dokuza kadar birimleri temsil eden dar, kama şeklindeki işaretlerden oluşan bir gruptan ( , , , , ..., ) ve beşe kadar onları temsil eden geniş, kama şeklindeki işaretlerden oluşan bir gruptan ( , , , , ) oluşuyordu. Rakamın değeri, bileşen parçalarının değerlerinin toplamıydı:
59'dan büyük sayılar, yer değeri gösteriminde bu biçimdeki birden fazla sembol bloğuyla gösterilmiştir . Sıfır için bir sembol olmadığından, bir sayının nasıl yorumlanması gerektiği her zaman hemen belli olmaz ve gerçek değeri bazen bağlamı tarafından belirlenmiş olabilir. Örneğin, 1 ve 60 için semboller aynıdır. [ 3 ] [ 4 ] Daha sonraki Babil metinleri sıfırı temsil etmek için bir yer tutucu ( ) kullanmıştır, ancak yalnızca orta konumlarda ve sayılarda olduğu gibi sayının sağ tarafında değil13 200 . [ 4 ]
Diğer tarihi kullanımlar
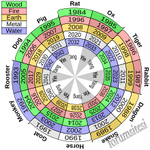
Çin burçlarındaki 5 elementin ve 12 hayvanın kombinasyonları 60 yıllık altmışlık döngüyü oluşturur
Çin takviminde , günlerin veya yılların on daldan oluşan bir dizideki ve 12 daldan oluşan başka bir dizideki pozisyonlara göre adlandırıldığı bir sistem yaygın olarak kullanılır. Aynı dal ve gövde bu döngü boyunca her 60 adımda bir tekrar eder.
Platon'un Devlet'inin VIII. Kitabı, 60 sayısına odaklanan bir evlilik alegorisini içerir . 4 =12 960 000 ve bölenleri. Bu sayının özellikle basit bir altmışlık gösterimi vardır: 1,0,0,0,0. Daha sonraki bilginler bu pasajı açıklamak için hem Babil matematiğine hem de müzik teorisine başvurdular. [ 5 ]
MS 2. yüzyılda yazılmış matematiksel astronomi üzerine bir inceleme olan Batlamyus'un Almagest'i , sayıların kesirli kısımlarını ifade etmek için 60 tabanını kullanır. Özellikle, esasen bir bin yıldan uzun bir süre boyunca tek kapsamlı trigonometrik tablo olan akor tablosu , 60 tabanında bir derecenin kesirli kısımlarına sahiptir ve pratik olarak sinüs fonksiyonunun modern bir değer tablosuna eşdeğerdir .
Ortaçağ gökbilimcileri de zamanı belirtmek için altmışlık sayıları kullandılar. El-Biruni, Yahudi aylarını tartışırken saati altmışlık sayılara bölerek ilk olarak 1000'de dakikalara , saniyelere , üçte birlere ve dörtte birlere böldü. [ 6 ] 1235 civarında Sacrobosco'lu John bu geleneği sürdürdü, ancak Nothaft bunu yapan ilk kişinin Sacrobosco olduğunu düşünüyordu. [ 7 ] Alfonsine tablolarının Paris versiyonu (yaklaşık 1320), günü temel zaman birimi olarak kullandı ve bir günün katlarını ve kesirlerini 60 tabanlı gösterimde kaydetti. [ 8 ]
Altmışlık sayı sistemi, 1671'e kadar Avrupalı gökbilimciler tarafından hesaplamalar yapmak için sıklıkla kullanılmaya devam etti. [ 9 ] Örneğin, Jost Bürgi , Fundamentum Astronomiae'de ( 1592'de İmparator II. Rudolf'a sunuldu ), meslektaşı Ursus, Fundamentum Astronomicum'da ve muhtemelen Henry Briggs de sinüsleri hesaplamak için 16. yüzyılın sonlarında altmışlık sisteme dayalı çarpım tablolarını kullandılar. [ 10 ]
18. yüzyılın sonu ve 19. yüzyılın başlarında, Tamil gökbilimcilerin, Helenistik gökbilimciler tarafından geliştirilen ondalık ve altmışlık gösterimlerin bir karışımını kullanarak kabuklarla hesaplamalar yaparak astronomik hesaplamalar yaptıkları bulundu . [ 11 ]
60 tabanlı sayı sistemleri Sümerlerle alakası olmayan bazı diğer kültürlerde de kullanılmıştır, örneğin Batı Yeni Gine'deki Ekari halkı tarafından . [ 12 ] [ 13 ]
Modern kullanım
Daha fazla bilgi: Derece (açı) § Alt bölümler , Arkın dakikası ve saniyesi , Saat , Dakika ve Saniye
Altmışlık sistemin modern kullanımları arasında açıların , coğrafi koordinatların , elektronik navigasyonun ve zamanın ölçülmesi yer alır . [ 14 ]
Bir saatlik zaman 60 dakikaya , bir dakika ise 60 saniyeye bölünür. Bu nedenle, 3:23:17 (3 saat, 23 dakika ve 17 saniye) gibi bir zaman ölçümü , tam bir altmışlık sayı (altmışlık nokta yok) olarak yorumlanabilir; bu da 3 × 60 2 + 23 × 60 1 + 17 × 60 0 saniye anlamına gelir. Ancak, bu sayıdaki üç altmışlık rakamın her biri (3, 23 ve 17) ondalık sistem kullanılarak yazılır .
Benzer şekilde, açısal ölçünün pratik birimi derecedir , bir dairede 360 (altı altmış) vardır . Bir derecede 60 yay dakikası ve bir dakikada 60 yay saniyesi vardır.
YAML
YAML veri depolama biçiminin 1.1 [ 15 ] sürümünde , altmışlık sayılar düz skalerler için desteklenir ve hem tam sayılar [ 16 ] hem de kayan nokta sayıları [ 17 ] için resmen belirtilir. Bu, örneğin bazı MAC adreslerinin altmışlık sayılar olarak tanınması ve tam sayılar olarak yüklenmesi, diğerlerinin ise tanınmaması ve dizeler olarak yüklenmesi gibi karışıklığa yol açmıştır . YAML 1.2'de altmışlık sayılar için destek kaldırıldı. [ 18 ]
Notasyonlar
Ayrıca bakınız: Pozisyonel gösterim § Altmışlık sistem
Ptolemaios'un yazıları gibi Helenistik Yunan astronomik metinlerinde , altmışlık sayılar Yunan alfabetik rakamları kullanılarak yazılırdı ve her altmışlık rakam ayrı bir sayı olarak ele alınırdı. Helenistik astronomlar sıfır için yeni bir sembol benimsediler,
—
°
, yüzyıllar boyunca Yunan harfi omikron, ο dahil olmak üzere diğer biçimlere dönüşmüştür, normalde 70 anlamına gelir, ancak herhangi bir konumdaki maksimum değerin 59 olduğu bir altmışlık sistemde izin verilir. [ 19 ] [ 20 ] Yunanlılar altmışlık sayıların kullanımını bir sayının kesirli kısmıyla sınırladılar. [ 21 ]
Ortaçağ Latin metinlerinde, altmışlık sayılar Arap rakamları kullanılarak yazılırdı ; kesirlerin farklı seviyeleri minuta (yani kesir), minuta secunda , minuta tertia , vb. olarak gösterilirdi. 17. yüzyılda, altmışlık sayıların tam kısmının üst simge sıfırla ve çeşitli kesirli kısımların bir veya daha fazla vurgu işaretiyle gösterilmesi yaygınlaştı. John Wallis , Mathesis universalis adlı eserinde bu gösterimi 60'ın daha yüksek katlarını da içerecek şekilde genelleştirdi; örnek olarak 49‵‵‵‵36‵‵‵25‵‵15‵1°15′2″36‴49⁗ sayısını verdi ; Soldaki sayılar 60'ın daha yüksek kuvvetleriyle çarpılırken, sağdaki sayılar 60'ın kuvvetlerine bölünür ve üst üste sıfırla işaretlenen sayı 1 ile çarpılır. [ 22 ] Bu gösterim, derece, dakika ve saniye için kullanılan modern işaretlere yol açar. Aynı dakika ve saniye adlandırması zaman birimleri için de kullanılır ve saat, dakika ve saniyelerin ondalık olarak yazıldığı ve iki nokta üst üste ile birbirinden ayrıldığı modern zaman gösterimi, altmışlık gösterim biçimi olarak yorumlanabilir.
Bazı kullanım sistemlerinde, altmışlık noktadan sonraki her pozisyon, Latince veya Fransızca kökler kullanılarak numaralandırılırdı: prime veya primus , seconde veya secundus , tierce , quatre , quinte , vb. Bugün bile bir saatin veya bir derecenin ikinci dereceden kısmına "saniye " diyoruz . En azından 18. yüzyıla kadar,
1
/
60
ikinciye "tierce" veya "üçüncü" deniyordu. [ 23 ] [ 24 ]
1930'larda Otto Neugebauer , her pozisyonda 0'dan 59'a kadar modern ondalık gösterimleri ikame eden, tam sayı ve kesirli kısımları ayırmak için noktalı virgül ( ve her kısmın içindeki pozisyonları ayırmak için virgül (,) kullanan Babil ve Helenistik sayılar için modern bir gösterim sistemi tanıttı. [ 25 ] Örneğin, hem Babil hem de Helenistik astronomlar tarafından kullanılan ve İbrani takviminde hala kullanılan ortalama sinodik ay 29;31,50,8,20 gündür. Bu gösterim bu makalede kullanılmıştır.
ve her kısmın içindeki pozisyonları ayırmak için virgül (,) kullanan Babil ve Helenistik sayılar için modern bir gösterim sistemi tanıttı. [ 25 ] Örneğin, hem Babil hem de Helenistik astronomlar tarafından kullanılan ve İbrani takviminde hala kullanılan ortalama sinodik ay 29;31,50,8,20 gündür. Bu gösterim bu makalede kullanılmıştır.
Kesirler ve irrasyonel sayılar
Kesirler
Altmışlık sistemde, paydası düzenli bir sayı olan ( asal çarpanlarına ayırmada yalnızca 2, 3 ve 5 bulunan ) herhangi bir kesir tam olarak ifade edilebilir. [ 26 ] Burada, paydası 60'tan küçük veya ona eşit olan bu türden tüm kesirler gösterilmektedir:
1 ⁄ 2 = 0;30
1 ⁄ 3 = 0;20
1 ⁄ 4 = 0;15
1 ⁄ 5 = 0;12
1 ⁄ 6 = 0;10
1 ⁄ 8 = 0;7,30
1 ⁄ 9 = 0;6,40
1 ⁄ 10 = 0;6
1 ⁄ 12 = 0;5
1 ⁄ 15 = 0;4
1 ⁄ 16 = 0;3,45
1 ⁄ 18 = 0;3,20
1 ⁄ 20 = 0;3
1 ⁄ 24 = 0;2,30
1 ⁄ 25 = 0;2,24
1 ⁄ 27 = 0;2,13,20
1 ⁄ 30 = 0;2
1 ⁄ 32 = 0;1,52,30
1 ⁄ 36 = 0;1,40
1 ⁄ 40 = 0;1,30
1 ⁄ 45 = 0;1,20
1 ⁄ 48 = 0;1,15
1 ⁄ 50 = 0;1,12
1 ⁄ 54 = 0;1,6,40
1 ⁄ 60 = 0;1
Ancak düzenli olmayan sayılar daha karmaşık tekrar eden kesirler oluşturur . Örneğin:
1 ⁄ 7 = 0; 8,34,17 (çubuk altmışlık basamak dizisini gösterir 8,34,17 sonsuz sayıda tekrar eder)
1 ⁄ 11 = 0; 5,27,16,21,49
1 ⁄ 13 = 0; 4,36,55,23
1 ⁄ 14 = 0;4, 17,8,34
1 ⁄ 17 = 0; 3,31,45,52,56,28,14,7
1 ⁄ 19 = 0; 3,9,28,25,15,47,22,6,18,56,50,31,34,44,12,37,53,41
1 ⁄ 59 = 0; 1
1 ⁄ 61 = 0; 0,59
Altmışa komşu olan 59 ve 61 sayılarının ikisinin de asal sayı olması, bir veya iki altmışlık basamaklı bir noktayla tekrar eden kesirlerin paydalarının yalnızca 59 veya 61'in normal sayı katları olabileceği ve diğer düzensiz sayıların daha uzun bir noktayla tekrar eden kesirlere sahip olabileceği anlamına gelir.
İrrasyonel sayılar
Altmışlık sayı sistemi 1;24,51,10'u gösteren ve √ 2'ye yaklaşan Babil tableti YBC 7289
Herhangi bir konumsal sayı sisteminde (ondalık ve altmışlık sayılar dahil) irrasyonel sayıların gösterimleri ne sonlanır ne de tekrarlanır .
Birim karenin köşegeninin uzunluğu olan 2'nin karekökü , Eski Babil Dönemi'ndeki ( MÖ 1900 - MÖ 1650 ) Babilliler tarafından yaklaşık olarak şu şekilde hesaplanmıştır:
1
;
24
,
51
,
10
=
1
+
24
60
+
51
60
2
+
10
60
3
=
30547
21600
≈
1.41421296
…
{\displaystyle 1;24,51,10=1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}={\frac {30547}{21600}}\yaklaşık 1,41421296\ldots }[ 27 ]
Çünkü √ 2 ≈ 1.414 213 56 ... irrasyonel bir sayıdır , tam olarak altmışlık sistemde (veya herhangi bir tam sayı tabanlı sistemde) ifade edilemez, ancak altmışlık sistemin genişlemesi 1;24,51,10,7,46,6,4,44... ( OEIS : A070197 ) ile başlar
Yunan matematikçi ve bilim adamı Batlamyus'un kullandığı π değeri 3;8,30 = 3 +
8
/
60
+
30
/
60 2
=
377
/
120
≈3.141 666 .... [ 28 ] 15. yüzyılda yaşamış bir Fars matematikçisi olan Cemşid el-Kaşî , 2 π'yi dokuz alt basamağa yuvarlandığında doğru değerine altmışlık bir ifade olarak hesapladı (böylece
1
/
60 9
); 2 π için değeri 6;16,59,28,1,34,51,46,14,50 idi. [ 29 ] [ 30 ] Yukarıdaki √ 2 gibi , 2 π irrasyonel bir sayıdır ve tam olarak altmışlık olarak ifade edilemez. Altmışlık açılımı 6;16,59,28,1,34,51,46,14,49,55,12,35... ( OEIS : A091649 )
Üstün, oldukça bileşik bir sayı olan 60 sayısının on iki böleni vardır : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ve 60; bunlardan 2, 3 ve 5 asal sayılardır . Bu kadar çok çarpanı olması nedeniyle, altmışlık sayıları içeren birçok kesir basitleştirilir. Örneğin, bir saat 30 dakika, 20 dakika, 15 dakika, 12 dakika, 10 dakika, 6 dakika, 5 dakika, 4 dakika, 3 dakika, 2 dakika ve 1 dakikalık bölümlere eşit olarak bölünebilir. 60, 1'den 6'ya kadar her sayıya bölünebilen en küçük sayıdır; yani, 1, 2, 3, 4, 5 ve 6'nın en küçük ortak katıdır .
Bu makalede, aksi belirtilmediği sürece tüm altmışlık basamaklar ondalık sayılar olarak temsil edilir. Örneğin, en büyük altmışlık basamak "59"dur.
Kökeni
Otto Neugebauer'e göre , altmışlık sayı sisteminin kökenleri, sıklıkla tasvir edildiği kadar basit, tutarlı veya zamansal olarak tekil değildir. Günümüzde zaman, açılar ve astronomik koordinat sistemleri gibi uzmanlaşmış konular için kullanılmaya devam eden yüzyıllar boyunca, altmışlık sayı sistemi gösterimleri, altmışlık sayı sisteminin nasıl yazıldığı gibi konularda her zaman güçlü bir ondalık gösterim alt akıntısı içermiştir. Kullanımları ayrıca, tek bir metin içinde bile sayıları temsil etmek için çeşitli tabanların nerede ve nasıl kullanılacağı konusunda tutarsızlıklar içermiştir (ve içermeye devam etmektedir). [ 2 ]
Erken Proto-çivi yazısı (M.Ö. 4. bin yıl) ve altmışlık sisteme ait çivi yazısı işaretleri (60, 600, 3600, vb.)
Altmışlık sistemin titiz ve tamamen kendi içinde tutarlı bir şekilde kullanılmasının en güçlü itici gücü, kesirleri yazma ve hesaplama konusundaki matematiksel avantajları olmuştur. Antik metinlerde bu, altmışlık sistemin matematiksel veri tablolarında en tekdüze ve tutarlı şekilde kullanılması gerçeğinde ortaya çıkar. [ 2 ] Altmışlık sistemin geçmişte matematiksel tablolarda olduğundan daha az tutarlı bir şekilde kullanılmasına rağmen kullanımının yaygınlaşmasına yardımcı olan bir diğer pratik faktör, büyük miktarlarda mal için pazarlık yapmayı ve bunları paylaşmayı içerdiğinde günlük finansal işlemleri kolaylaştırması açısından tüccarlar ve alıcılar için belirgin avantajlarıydı. MÖ 3. binyılın sonlarında, Sümer/Akad ağırlık birimleri, 60 manû'ya ( mina ) bölünen kakkaru'yu ( talent , yaklaşık 30 kg) içeriyordu ve bu da daha sonra 60 šiqlu'ya ( şekel ) bölündü ; bu birimlerin torunları binlerce yıl boyunca varlığını sürdürdü, ancak Yunanlılar daha sonra bu ilişkiyi bir şekelin bir minanın 50'de biri olduğu daha taban-10 uyumlu bir orana zorladı .
Matematiksel tabloların dışında, sayıların çoğu metinde nasıl temsil edildiğine ilişkin tutarsızlıklar , sayısal nicelikleri temsil etmek için kullanılan en temel çivi yazısı sembollerine kadar uzanıyordu . [ 2 ] Örneğin, 1 için çivi yazısı sembolü, kalem ucunun yuvarlak ucunun kile açılı olarak uygulanmasıyla oluşturulan bir elips iken, 60 için altmışlık sembol daha büyük bir oval veya "büyük 1" idi. Ancak bu sembollerin kullanıldığı aynı metinlerde, 10 sayısı, stilin yuvarlak ucunun kile dik olarak uygulanmasıyla oluşturulan bir daire olarak temsil ediliyordu ve 100'ü temsil etmek için daha büyük bir daire veya "büyük 10" kullanılıyordu. Bu tür çok tabanlı sayısal nicelik sembolleri, tek bir sayı içinde bile birbirleriyle ve kısaltmalarla karıştırılabiliyordu. Ayrıntılar ve hatta ima edilen büyüklükler ( sıfır tutarlı bir şekilde kullanılmadığından ) temsil edilen belirli zaman dilimlerine, kültürlere ve niceliklere veya kavramlara özgüydü. Sayısal niceliklerin bu tür bağlam-bağımlı temsillerinin geriye dönüp bakıldığında eleştirilmesi kolay olsa da, modern zamanlarda, altmışlık astronomik koordinatlara ondalık kesirlerin eklenmesi gibi son yenilikler de dahil olmak üzere, konuya-bağımlı temel karıştırmanın düzenli olarak kullanılan düzinelerce örneğine hâlâ sahibiz. [ 2 ]
Kullanım
Babil matematiği
Ana madde: Babil çivi yazısı rakamları
Antik Mezopotamya'da kullanılan altmışlık sistem , rakamları için 60 ayrı sembol kullanmadığı anlamında saf bir 60 tabanlı sistem değildi . Bunun yerine, çivi yazısı rakamları bir işaret-değer gösterimi tarzında alt taban olarak on kullanıyordu : bir altmışlık rakam, dokuza kadar birimleri temsil eden dar, kama şeklindeki işaretlerden oluşan bir gruptan ( , , , , ..., ) ve beşe kadar onları temsil eden geniş, kama şeklindeki işaretlerden oluşan bir gruptan ( , , , , ) oluşuyordu. Rakamın değeri, bileşen parçalarının değerlerinin toplamıydı:
59'dan büyük sayılar, yer değeri gösteriminde bu biçimdeki birden fazla sembol bloğuyla gösterilmiştir . Sıfır için bir sembol olmadığından, bir sayının nasıl yorumlanması gerektiği her zaman hemen belli olmaz ve gerçek değeri bazen bağlamı tarafından belirlenmiş olabilir. Örneğin, 1 ve 60 için semboller aynıdır. [ 3 ] [ 4 ] Daha sonraki Babil metinleri sıfırı temsil etmek için bir yer tutucu ( ) kullanmıştır, ancak yalnızca orta konumlarda ve sayılarda olduğu gibi sayının sağ tarafında değil13 200 . [ 4 ]
Diğer tarihi kullanımlar
Çin burçlarındaki 5 elementin ve 12 hayvanın kombinasyonları 60 yıllık altmışlık döngüyü oluşturur
Çin takviminde , günlerin veya yılların on daldan oluşan bir dizideki ve 12 daldan oluşan başka bir dizideki pozisyonlara göre adlandırıldığı bir sistem yaygın olarak kullanılır. Aynı dal ve gövde bu döngü boyunca her 60 adımda bir tekrar eder.
Platon'un Devlet'inin VIII. Kitabı, 60 sayısına odaklanan bir evlilik alegorisini içerir . 4 =12 960 000 ve bölenleri. Bu sayının özellikle basit bir altmışlık gösterimi vardır: 1,0,0,0,0. Daha sonraki bilginler bu pasajı açıklamak için hem Babil matematiğine hem de müzik teorisine başvurdular. [ 5 ]
MS 2. yüzyılda yazılmış matematiksel astronomi üzerine bir inceleme olan Batlamyus'un Almagest'i , sayıların kesirli kısımlarını ifade etmek için 60 tabanını kullanır. Özellikle, esasen bir bin yıldan uzun bir süre boyunca tek kapsamlı trigonometrik tablo olan akor tablosu , 60 tabanında bir derecenin kesirli kısımlarına sahiptir ve pratik olarak sinüs fonksiyonunun modern bir değer tablosuna eşdeğerdir .
Ortaçağ gökbilimcileri de zamanı belirtmek için altmışlık sayıları kullandılar. El-Biruni, Yahudi aylarını tartışırken saati altmışlık sayılara bölerek ilk olarak 1000'de dakikalara , saniyelere , üçte birlere ve dörtte birlere böldü. [ 6 ] 1235 civarında Sacrobosco'lu John bu geleneği sürdürdü, ancak Nothaft bunu yapan ilk kişinin Sacrobosco olduğunu düşünüyordu. [ 7 ] Alfonsine tablolarının Paris versiyonu (yaklaşık 1320), günü temel zaman birimi olarak kullandı ve bir günün katlarını ve kesirlerini 60 tabanlı gösterimde kaydetti. [ 8 ]
Altmışlık sayı sistemi, 1671'e kadar Avrupalı gökbilimciler tarafından hesaplamalar yapmak için sıklıkla kullanılmaya devam etti. [ 9 ] Örneğin, Jost Bürgi , Fundamentum Astronomiae'de ( 1592'de İmparator II. Rudolf'a sunuldu ), meslektaşı Ursus, Fundamentum Astronomicum'da ve muhtemelen Henry Briggs de sinüsleri hesaplamak için 16. yüzyılın sonlarında altmışlık sisteme dayalı çarpım tablolarını kullandılar. [ 10 ]
18. yüzyılın sonu ve 19. yüzyılın başlarında, Tamil gökbilimcilerin, Helenistik gökbilimciler tarafından geliştirilen ondalık ve altmışlık gösterimlerin bir karışımını kullanarak kabuklarla hesaplamalar yaparak astronomik hesaplamalar yaptıkları bulundu . [ 11 ]
60 tabanlı sayı sistemleri Sümerlerle alakası olmayan bazı diğer kültürlerde de kullanılmıştır, örneğin Batı Yeni Gine'deki Ekari halkı tarafından . [ 12 ] [ 13 ]
Modern kullanım
Daha fazla bilgi: Derece (açı) § Alt bölümler , Arkın dakikası ve saniyesi , Saat , Dakika ve Saniye
Altmışlık sistemin modern kullanımları arasında açıların , coğrafi koordinatların , elektronik navigasyonun ve zamanın ölçülmesi yer alır . [ 14 ]
Bir saatlik zaman 60 dakikaya , bir dakika ise 60 saniyeye bölünür. Bu nedenle, 3:23:17 (3 saat, 23 dakika ve 17 saniye) gibi bir zaman ölçümü , tam bir altmışlık sayı (altmışlık nokta yok) olarak yorumlanabilir; bu da 3 × 60 2 + 23 × 60 1 + 17 × 60 0 saniye anlamına gelir. Ancak, bu sayıdaki üç altmışlık rakamın her biri (3, 23 ve 17) ondalık sistem kullanılarak yazılır .
Benzer şekilde, açısal ölçünün pratik birimi derecedir , bir dairede 360 (altı altmış) vardır . Bir derecede 60 yay dakikası ve bir dakikada 60 yay saniyesi vardır.
YAML
YAML veri depolama biçiminin 1.1 [ 15 ] sürümünde , altmışlık sayılar düz skalerler için desteklenir ve hem tam sayılar [ 16 ] hem de kayan nokta sayıları [ 17 ] için resmen belirtilir. Bu, örneğin bazı MAC adreslerinin altmışlık sayılar olarak tanınması ve tam sayılar olarak yüklenmesi, diğerlerinin ise tanınmaması ve dizeler olarak yüklenmesi gibi karışıklığa yol açmıştır . YAML 1.2'de altmışlık sayılar için destek kaldırıldı. [ 18 ]
Notasyonlar
Ayrıca bakınız: Pozisyonel gösterim § Altmışlık sistem
Ptolemaios'un yazıları gibi Helenistik Yunan astronomik metinlerinde , altmışlık sayılar Yunan alfabetik rakamları kullanılarak yazılırdı ve her altmışlık rakam ayrı bir sayı olarak ele alınırdı. Helenistik astronomlar sıfır için yeni bir sembol benimsediler,
—
°
, yüzyıllar boyunca Yunan harfi omikron, ο dahil olmak üzere diğer biçimlere dönüşmüştür, normalde 70 anlamına gelir, ancak herhangi bir konumdaki maksimum değerin 59 olduğu bir altmışlık sistemde izin verilir. [ 19 ] [ 20 ] Yunanlılar altmışlık sayıların kullanımını bir sayının kesirli kısmıyla sınırladılar. [ 21 ]
Ortaçağ Latin metinlerinde, altmışlık sayılar Arap rakamları kullanılarak yazılırdı ; kesirlerin farklı seviyeleri minuta (yani kesir), minuta secunda , minuta tertia , vb. olarak gösterilirdi. 17. yüzyılda, altmışlık sayıların tam kısmının üst simge sıfırla ve çeşitli kesirli kısımların bir veya daha fazla vurgu işaretiyle gösterilmesi yaygınlaştı. John Wallis , Mathesis universalis adlı eserinde bu gösterimi 60'ın daha yüksek katlarını da içerecek şekilde genelleştirdi; örnek olarak 49‵‵‵‵36‵‵‵25‵‵15‵1°15′2″36‴49⁗ sayısını verdi ; Soldaki sayılar 60'ın daha yüksek kuvvetleriyle çarpılırken, sağdaki sayılar 60'ın kuvvetlerine bölünür ve üst üste sıfırla işaretlenen sayı 1 ile çarpılır. [ 22 ] Bu gösterim, derece, dakika ve saniye için kullanılan modern işaretlere yol açar. Aynı dakika ve saniye adlandırması zaman birimleri için de kullanılır ve saat, dakika ve saniyelerin ondalık olarak yazıldığı ve iki nokta üst üste ile birbirinden ayrıldığı modern zaman gösterimi, altmışlık gösterim biçimi olarak yorumlanabilir.
Bazı kullanım sistemlerinde, altmışlık noktadan sonraki her pozisyon, Latince veya Fransızca kökler kullanılarak numaralandırılırdı: prime veya primus , seconde veya secundus , tierce , quatre , quinte , vb. Bugün bile bir saatin veya bir derecenin ikinci dereceden kısmına "saniye " diyoruz . En azından 18. yüzyıla kadar,
1
/
60
ikinciye "tierce" veya "üçüncü" deniyordu. [ 23 ] [ 24 ]
1930'larda Otto Neugebauer , her pozisyonda 0'dan 59'a kadar modern ondalık gösterimleri ikame eden, tam sayı ve kesirli kısımları ayırmak için noktalı virgül (
Kesirler ve irrasyonel sayılar
Kesirler
Altmışlık sistemde, paydası düzenli bir sayı olan ( asal çarpanlarına ayırmada yalnızca 2, 3 ve 5 bulunan ) herhangi bir kesir tam olarak ifade edilebilir. [ 26 ] Burada, paydası 60'tan küçük veya ona eşit olan bu türden tüm kesirler gösterilmektedir:
1 ⁄ 2 = 0;30
1 ⁄ 3 = 0;20
1 ⁄ 4 = 0;15
1 ⁄ 5 = 0;12
1 ⁄ 6 = 0;10
1 ⁄ 8 = 0;7,30
1 ⁄ 9 = 0;6,40
1 ⁄ 10 = 0;6
1 ⁄ 12 = 0;5
1 ⁄ 15 = 0;4
1 ⁄ 16 = 0;3,45
1 ⁄ 18 = 0;3,20
1 ⁄ 20 = 0;3
1 ⁄ 24 = 0;2,30
1 ⁄ 25 = 0;2,24
1 ⁄ 27 = 0;2,13,20
1 ⁄ 30 = 0;2
1 ⁄ 32 = 0;1,52,30
1 ⁄ 36 = 0;1,40
1 ⁄ 40 = 0;1,30
1 ⁄ 45 = 0;1,20
1 ⁄ 48 = 0;1,15
1 ⁄ 50 = 0;1,12
1 ⁄ 54 = 0;1,6,40
1 ⁄ 60 = 0;1
Ancak düzenli olmayan sayılar daha karmaşık tekrar eden kesirler oluşturur . Örneğin:
1 ⁄ 7 = 0; 8,34,17 (çubuk altmışlık basamak dizisini gösterir 8,34,17 sonsuz sayıda tekrar eder)
1 ⁄ 11 = 0; 5,27,16,21,49
1 ⁄ 13 = 0; 4,36,55,23
1 ⁄ 14 = 0;4, 17,8,34
1 ⁄ 17 = 0; 3,31,45,52,56,28,14,7
1 ⁄ 19 = 0; 3,9,28,25,15,47,22,6,18,56,50,31,34,44,12,37,53,41
1 ⁄ 59 = 0; 1
1 ⁄ 61 = 0; 0,59
Altmışa komşu olan 59 ve 61 sayılarının ikisinin de asal sayı olması, bir veya iki altmışlık basamaklı bir noktayla tekrar eden kesirlerin paydalarının yalnızca 59 veya 61'in normal sayı katları olabileceği ve diğer düzensiz sayıların daha uzun bir noktayla tekrar eden kesirlere sahip olabileceği anlamına gelir.
İrrasyonel sayılar
Altmışlık sayı sistemi 1;24,51,10'u gösteren ve √ 2'ye yaklaşan Babil tableti YBC 7289
Herhangi bir konumsal sayı sisteminde (ondalık ve altmışlık sayılar dahil) irrasyonel sayıların gösterimleri ne sonlanır ne de tekrarlanır .
Birim karenin köşegeninin uzunluğu olan 2'nin karekökü , Eski Babil Dönemi'ndeki ( MÖ 1900 - MÖ 1650 ) Babilliler tarafından yaklaşık olarak şu şekilde hesaplanmıştır:
1
;
24
,
51
,
10
=
1
+
24
60
+
51
60
2
+
10
60
3
=
30547
21600
≈
1.41421296
…
{\displaystyle 1;24,51,10=1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}={\frac {30547}{21600}}\yaklaşık 1,41421296\ldots }[ 27 ]
Çünkü √ 2 ≈ 1.414 213 56 ... irrasyonel bir sayıdır , tam olarak altmışlık sistemde (veya herhangi bir tam sayı tabanlı sistemde) ifade edilemez, ancak altmışlık sistemin genişlemesi 1;24,51,10,7,46,6,4,44... ( OEIS : A070197 ) ile başlar
Yunan matematikçi ve bilim adamı Batlamyus'un kullandığı π değeri 3;8,30 = 3 +
8
/
60
+
30
/
60 2
=
377
/
120
≈3.141 666 .... [ 28 ] 15. yüzyılda yaşamış bir Fars matematikçisi olan Cemşid el-Kaşî , 2 π'yi dokuz alt basamağa yuvarlandığında doğru değerine altmışlık bir ifade olarak hesapladı (böylece
1
/
60 9
); 2 π için değeri 6;16,59,28,1,34,51,46,14,50 idi. [ 29 ] [ 30 ] Yukarıdaki √ 2 gibi , 2 π irrasyonel bir sayıdır ve tam olarak altmışlık olarak ifade edilemez. Altmışlık açılımı 6;16,59,28,1,34,51,46,14,49,55,12,35... ( OEIS : A091649 )